原码反码补码

原码

1. 十进制数据的二进制表现形式，最左边是符号位，0为正，1为负

2. 利用原码对正数进行计算是不会出现问题的。

3. 但是如果是负数计算，结果就会出错，实际运算的结果，跟我们预期的结果是相反的。

​ 在计算机中1个0或者1个1，我们称为bit(比特位)，把八个比特位称为一个字节（1byte = 8bit），是计算机中最小的存储单元。

​ 一个字节的最大值为01111111，转成十进制是+127，最小值是11111111，转成十进制是-127

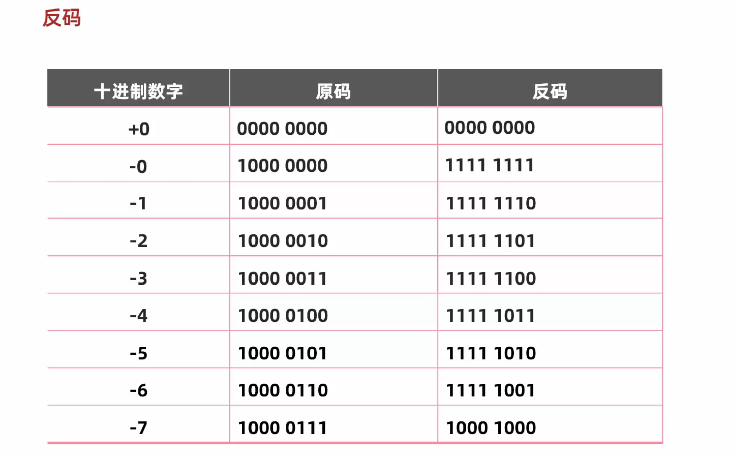
反码

​ 为了解决原码不能计算负数的问题而出现的

计算规则

​ 正数的反码不变，负数的反码在原码的基础上，符号位不变。数值取反，0变1,1变0

补码

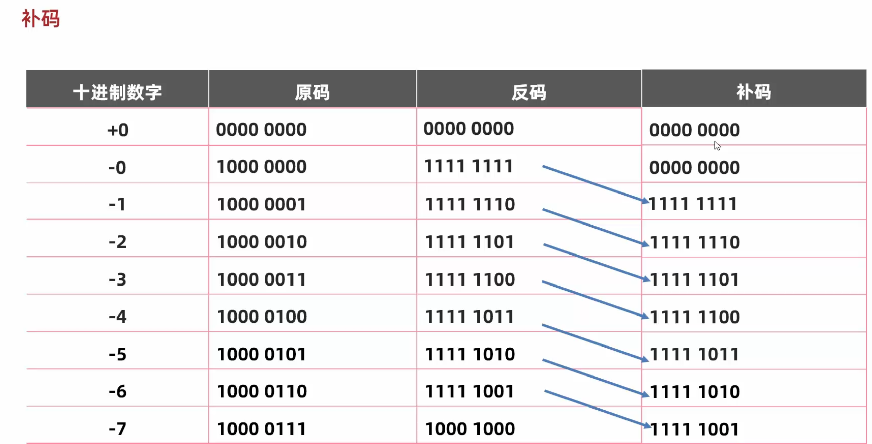
为了解决负数计算时跨0的问题而出现的

由于在反码中0有两种表现形式，分别为00000000,、11111111，如果只在负数层面上进行计算，不会出现问题，如果计算需要从负数跨越到正数，则会结果不对（结果小1），所以为了解决这个问题，出现了补码（在反码的基础上+1）

补码的计算规则

• 正数的补码不变，负数的补码在反码的基础上+1
• 另外补码还能多记录一个特殊的数值-128，该数据在一个字节下，没有原码和反码

补码的注意点

​ 1.计算机中的存储和计算都是以补码的形式进行的

​ 2.正数的原码、反码、补码都一样

延伸

基本数据类型

• byte类型的10 1个字节 0000 1010
• short类型的10 2个字节 0000 0000 0000 1010
• int类型的10 4个字节 0000 0000 0000 0000 0000 0000 0000 1010
• long类型的10 8个字节 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 1010

由上可知，类型转换就是补足多出来的比特位,所以低转高，可以隐式转换，不丢失精度，而高转低，需要强制转换，因为会丢失精度